DSTAIR: A Decision Support Tool to Analyze Institutional Reform

Click here to go back to "About DSTAIR"

Within any given sphere (e.g., legislative, economic, judicial), corruption is largely the outcome of a breakdown in legitimate or just institutions (i.e., formal and informal rules, habits--North, 1990), leading to unfair or arbitrary institutions. This is not to deny the important role of individuals as agents of corruption; nevertheless, corrupt behavior is most likely to take place routinely only in those circumstances where prevailing rules and practices either fail to prevent it or actively condone it. In some instances, the ambiguity of conflicting institutions in overlapping domains, or the absence of clarity in the rules, could also increase the scope for corruption. Thus, it is the institutional failure to stem the routine use of public resources for private gain that amounts to the breach of public trust that we term corruption. Such a breach of trust could occur at various sites within the entire network of social, economic and political relationships within a country (see Figure).

The conceptual model used here conceives of the social, economic and political spheres of any given country as constituting a system with institutional flows. Barriers, blockages and diversions of these flows appear figuratively as "breaches", and more specifically as opportunities for increasing corruption.

DSTAIR is a Decision Support Tool to Analyze Institutional Reform. The tool merely assists analysts and country experts in generating "legitimacy" scores for different spheres of government, civil society and economic activity within a country based on the ratings they provide to questions relating to institutional arrangements. Where these arrangements (rules and practices) are robust, the user is encouraged to assign a high rating. Where these are poor, the rating is expected to be low. Aggregate and normalized scores based on the ratings provide the user a quick view of the legitimacy of different spheres. The user may then examine a suite of anti-corruption tools that could be deployed in response, and review case studies appropriate to each tool in order to gain a fuller appreciation of past applications of the tool. DSTAIR also provides the user with an indication of which anti-corruption tools most likely to be of value, based on the particular combination of legitimacy scores earned by the different spheres.

DSTAIR is currently divided into nine "spheres": Constitution, Legislature, Executive, Administration, Judiciary, Political Parties, Civil Society, Economic Sphere, and Media. The premise is that each sphere operates through a finite set of especially important institutional arrangements, and that when the "quality" of several of these arrangements suffers, the legitimacy of the sphere as a whole is adversely affected. Moreover, bad institutional effects can "propagate" to other spheres. For example, a Judiciary that has a poor system of judicial appointment not only diminishes its own legitimacy but also reflects badly on the Legislature, the Executive and the Constitution.

The institutional arrangements relevant to each sphere are as follows: one set concerns the legitimacy of the "meta-rules," i.e., the institutions that are important for formation of the sphere itself (e.g., judicial appointments); another set determines the legitimacy of the rules developed by the sphere (e.g., judgments); a third concerns exogenous factors (e.g., intimidation of judges by rogue elements in civil society). The user assigns scores and weights for all these arrangements. Advanced users could also determine the relative weights of the influence of/from other spheres of specific arrangements. A normalized score of legitimacy within each sphere is thereby derived.

Note that legitimacy, as defined here, stands for a combined measure of the effectiveness and legitimacy of the rules making up each sphere and the rules it generates, as well as some exogenous factors that cannot necessarily be changed by institutional design, like wars or resource problems. But this can also be "attenuated" by the legitimacy of other spheres, and so there is some limited modeling of the interaction among the spheres. For instance, a bad Constitution will have an impact on the legitimacy of the Economic sphere to the extent that there are rule linkages between the two.

A set of 28 anti-corruption tools, each of which require that legitimacy scores in the nine spheres are greater than pre-specified threshold levels in order that the tool be "triggered," are then compared against the scores. In the current version, the threshold values of legitimacy scores are based entirely on the developers' judgment, but will be modified with the help of expert advice others. Since the institutional scores are all normalized between 0 and 1, it is likely that after gaining some experience using DSTAIR, expert judgment will likely converge on the best threshold levels to adopt.

For each sphere, a aggregate rating { I j } for each sphere is first computed by adding up that sphere?s weighted scores (i.e, rating multiplied by importance level -? low = 1, medium = 2, and high = 3). These are "normalized" with respect to the maximum possible scores to get a result between 0 and 1. The internal score is then "attenuated" based on the level of influence from other spheres. In principle, the legitimacy of any given sphere can be affected by nearly any other--the level of influence is something that advanced users may decide to alter. Computationally, these influences are currently hard-wired to play only a small role in altering the final legitimacy score, but this effect may be changed in future versions based on suggestions from users.

The internal calculations carried out are as follows:

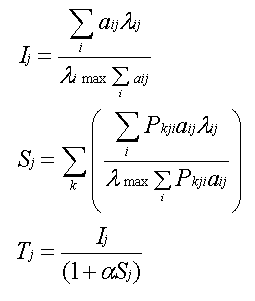
Where the variables are defined as follows:

i is an index over the institutional arrangements (total of 12 to 15 for each sphere)

j and k are indices over the spheres (total of 8),

T_j is the legitimacy of a given sphere j.

I_j is the weighted aggregate rating of the institutional arrangements for sphere j,

S_j is the cross-sphere interaction, reflecting the degree of influence on sphere j of institutional arrangements for the other spheres, k≠j

P_ijk the degree of influence on sphere j of institutional arrangement k for sphere i

λ_ij (lambda) is the rating (1-10) for a given institutional arrangement i and sphere j,

λ_max (lambda max) equals 10, a normalizing factor,

a_ij is the level of importance for a particular question (assigned 1,2,or 3 for low, medium and high, respectively) for a given instituational arrangement i and sphere j,

α (alpha) is a weighting factor (currently set at 0) reflecting the degree of 'attenuation' caused by interactive effects between spheres (currently, that can be adjusted only within the program).

Bardhan, Pranab (1997), "Corruption and Development: A Review of Issues," Journal of Economic Literature, Vol. XXXV (September 1997), pp. 1320-1346.
(http://ideas.repec.org/a/aea/jeclit/v35y1997i3p1320-1346.html)

Heidenheimer, Arnold and Michael Johnston (2001), Political Corruption, 3rd edition. Transaction Publishers, New Brunswick, NJ, 970p.

North, Douglass (1990), Institutions, Institutional Change and Economic Performance. Cambridge University Press, Cambridge, UK, 159p.

Rose-Ackerman, Susan (1999), Corruption and Government: Causes, Consequences and Reform, Cambridge University Press, Cambridge, UK, 280p.

Transparency International (2004), Global Corruption Report 2004, Pluto Press, London, 353p. Available at https://www.transparency.org/en/publications/global-corruption-report-2004-political-corruption.

United Nations Office of Drugs and Crime (2004): The United Nations Anti-Corruption Toolkit, 2nd edition (draft), Vienna, 654p.